Exo maths laboratoire

[Marc32]

Salut Job, j'espère que tu va bien, ça fais longtemps

Sinon j'ai fais cet exo, mais pourrait corrigé mes réponses stp?

version image de l'énoncé :

Même chose à l'écrit
Exercice 9: Un biologiste souhaite réaliser une analyse de sang. Il achète des pipettes de laboratoire soit dans une grande surface spécialisée soit dans une pharmacie. L'objectif est de comparer les prix proposés par ces deux fournisseurs.
En grande surface le prix est de 52 euros la pipette.

Dans la pharmacie, en raison des frais occasionnées, le prix de la pipette est donné par: g(x)=x^3-18x2+108x où z désigne la quantité de pipettes achetées. Etude de la fonction g sur l'intervalle [0, +00[

a) Déterminer la limite de g en +00.
b) Calculer la dérivée, étudier le signe de g et dresser son tableau de variation. Comparaison des deur prix proposés.

Soit f(x) le prix en grande surface, où z désigne la quantité de pipettes achetées. Soit à la fonction définie sur [0, +ool par: h(x) = g(x) - f(x).
a) Donner l'expression de h(x) en fonction de z et étudier le signe de h sur l'intervalle [0, +∞0[.

b) Déterminer l'intervalle pour le(s)equel(s) il est plus économique pour le biologiste de s'approvisionner à la pharmacie.
Mes réponses :

le tableau de variation c'est simple il n'y a qu'une racine, la fonction s'annule qu'une fois

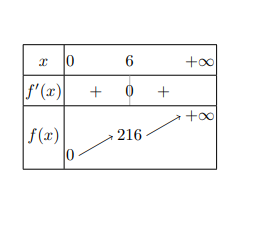la fonction est croissante sur l'intervalle 0 l'infini mais pas strictement croissante puisqu'elle s'annule.

Les autres question j'ai pas trouver..

[Job]

Bonjour Marc

Pour trouver le signe de $h(x)$, il faut calculer la dérivée, déterminer son signe et en déduire le tableau de variation de $h$.
C'est la même méthode que ce que tu as fait pour la fonction $g$

(Attention à bien conserver les noms donnés aux fonctions)

[Marc32]

Merci Job j'avais loupé cette question , voici ma réponse : https://ibb.co/PhPYVXc

[Job]

C'est exact. A partir de là, on peut répondre à la suite des questions.

[Amine]

Bonjour,
Calculer la dérivée pour déterminer le signe de h′(x) est une méthode précieuse, non seulement pour établir le tableau de variation de h, mais aussi pour approfondir notre compréhension des comportements des fonctions, similaire à l'approche que j'ai employée pour la fonction g. En intégrant ces techniques mathématiques, nous pouvons mieux appréhender les variations des fonctions.
Il est important de rappeler, tout comme dans les jeux de casino en ligne où chaque mouvement compte, que chaque étape de ce processus mathématique est cruciale. Cependant, il est essentiel de rester vigilant et de prévenir l'addiction au casino comme le souligne cette page, en gardant à l'esprit que derrière chaque jeu, il y a des risques significatifs

[elodie2]

Je viens d'avoir une solution à un problème qui me dérangeais grâce à cette exercice